An army of gamblers and a martingale

September 22, 2012 at 9:12 pm (markov chain, probability, Uncategorized)
Tags: , , ,

coin toss
Start flipping a coin. How long should you wait (on average) before observing the pattern {HHTHHTT} !? Easy you might say, that’s simply the hitting time of the state {H} starting from state {A} of the following Markov chain.

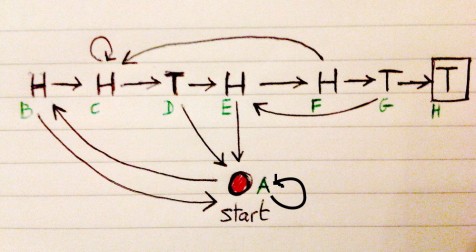
Indeed, one can solve this kind of problem using a first step analysis. In other words, if {a} is the expected number of steps before reaching {H} starting from {A}, {b} is the expected number of steps before reaching {H} starting from {B}, {c} is the expected number of steps before reaching {H} starting from {C}, etc… one can readily see that {a,b, \ldots, h} verify the system of equations

\displaystyle \begin{array}{rcl} a &=& 1 + \frac12(a+b), \quad b = 1 + \frac12(a+c), \quad c = 1 + \frac12(c+d) \\ d &=& 1 + \frac12(a+e), \quad e = 1 + \frac12(a+f), \quad f = 1 + \frac12(c+g) \\ g &=& 1 + \frac12(e+h), \quad h = 0. \end{array}

After a finite amount of time and coffee one then come up with the answer {a=128}. That was a little bit tedious and I don’t really want to know how long one should wait on average before observing the sequence {HHTHTTTHTHHHHTTHTHTTH}.

It turns out that there is a very neat way to approach this kind of problems without solving any linear system. Apparently, this trick was discovered in the 80s by Shuo-Yen Robert Li. As often in probability, this boils down to introducing a clever martingale. Suppose that one wants to know how long it takes on average before observing the magic coin pattern {x_1x_2 \ldots x_n} of length {n \geq 1} with {x_i \in \{H,T\}} for all {1 \leq i \leq n}. To this end, one will introduce an army of gamblers, a casino, a game of chance and a martingale. The martingale {M} describes the amount of money earned by the casino. At each round (starting at round {t=1}) the casino tosses a coin and the gamblers can make bets. If a gambler starts betting just before round {k}, he wins if the coin shows {x_1}. If he decides to bet again at round {k+1}, he wins if the coin shows {x_2}, etc… Suppose that there are infinitely many gamblers {G_0, G_1, G_2, \ldots} and that gambler {G_k} starts betting just before round {k+1}. The game is fair in the sense that if a gambler bets an amount {A}, with probability {1/2} he gets {2A} and with probability {1/2} he losses his bet. One supposes that gambler {G_k} starts betting {1} dollar just before round {k+1} and keeps reinvesting his total capital until he either losses everything (total loss equals {1} dollar) or observes the magic coin pattern {x_1x_2 \ldots x_n} (total earning equals {2^n-1}). Indeed, the amount of money earned by the casino is a martingale and {M_0=0}. For example, {M_1=1} if the first gambler {G_0} loses his bet and {M_1=-1} if the wins. Consider the time {\tau} when the magic coin pattern first appears. This is a stopping time and the optional stopping theorem for martingales shows that {\mathbb{E}[M_{\tau}] = 0}. Indeed, one can also compute this quantity another way. By time {\tau}, all the losers have given {1} dollar to the casino. Also, if the gambler {G_k} is still in the game he has won a total amount {2^{\tau-k}-1}. in other words,

\displaystyle M_{\tau} = \tau - \sum_{j=0}^{\tau-1} 2^{\tau-k} \, \delta_j

where {\delta_j=1} if the gambler {G_j} is still in the game after the round {\tau} and {\delta_j=0} otherwise. The fundamental remark is that the quantity {\sum_{j=1}^{\tau} 2^{\tau-k+1} \, \delta_j} is not random so that {\mathbb{E}[\tau] = \sum_{j=0}^{\tau-1} 2^{\tau-k} \, \delta_j}. Indeed, right after round {\tau} one can know with certainty whether {G_{k}} is still in the game or not. Gambler {G_{\tau-k}} is in the game only if the {k} last letters of the magic word {x_1x_2 \ldots x_n} are the same as the first {k} letters. For example, if the magic word is {HHTHHTH} then the gamblers who have seen the pattern {H},{HHTH} and {HHTHHTH} at time {\tau} are still in the game when the magic word first appear. In this case this shows that {\mathbb{E}[\tau] = 2^1+2^4+2^7}.

gambler

For example, this immediately shows that we have to wait on average {2^{21}+2^1} coin tosses before observing the pattern {HHTHTTTHTHHHHTTHTHTTH}.

4 Comments

Curvature for Markov Chains

March 21, 2011 at 2:19 pm (curvature, markov chain, Markov process, probability, Stochastic analysis, Uncategorized)
Tags: , , , , ,

Recently, Yann Ollivier developed a nice theory of Ricci curvature for Markov chains. In many ways, this can be seen as a geometric language giving another view on the notion of path coupling, developed at the end of the {90}‘s by Martin Dyer and co-workers. It has to be noted that this new notion of curvature is very general and does not need the state space where the Markov chain evolves to have any differential structure, as can be expected at first sight. Any state space endowed with a metric suffices.

Let {P} be a Markov kernel on a metric state space {(S,d)}. We would like to quantify how long it takes for two different particles evolving according to the Markovian dynamic given by {P} to meet. If the first particle starts at {x \in S} and the second at {y \in S}, the initial distance between them is {d(x,y)}. At time {t>0}, what is the average distance between these two particles. For example, if {W^x} and {W^y} are two Brownian motions in {{\mathbb R}^n} started from {x} and {y} respectively, there is no reason why {W^x_t} and {W^y_t} should be closer from each other than {x=W^x_0} and {y=W^y_0}. Indeed, one can even show that whatever the coupling of these two Brownian motions we have {\mathop{\mathbb E}[d(W^x_t, W^y_t)] \geq d(x,y)}: this is roughly speaking because the Euclidean space {{\mathbb R}^n} has no curvature. The situation is quite different if we were instead considering Brownian motions on a sphere: in this case, trajectories tend to coalesce.

1. Wasserstein distance

In the sequel, we will need to use a notion of distance between probability distributions on the metric space {(S,d)}. The usual total variation distance {d(\mu,\nu)} defined by

\displaystyle d(\mu,\nu) \;=\; \sup_{A \subset S} \; |\mu(A)-\nu(A)| \ \ \ \ \ (1)

is not adapted to our purpose since the metric structure of the space is not exploited. Instead, in order to take into account the distance {d(\cdot,\cdot)} of the space {E} and develop a notion of curvature, we use the Wasserstein distance {W(\mu,\nu)} between probability measures. It is defined as

\displaystyle W(\mu,\nu) \;=\; \sup\Big\{ \mu(f) - \nu(f) \;:\; \text{Lip}(f) \leq 1\Big\}. \ \ \ \ \ (2)

The distance {d(\cdot,\cdot)} is crucial to this definition: a change of distance implies a change of the class of {1}-Lipschitz functions. Since {\mu(f) - \nu(f) = \mathop{\mathbb E}[f(X) - f(Y)]} for any coupling {(X,Y)} of {\mu} and {\nu}, and since the function {f} is {1}-Lipschitz, it follows that {\mathop{\mathbb E}[f(X) - f(Y)] \leq \mathop{\mathbb E}[d(X,Y)]}. Consequently, for any coupling {(X,Y)} we have {W(\mu,\nu) \leq \mathop{\mathbb E}[d(X,Y)]}. Taking the infimum over all the couplings {(X,Y)} leads to the inequality

\displaystyle W(\mu,\nu) \;=\; \sup_{\text{Lip}(f) \leq 1} \; |\mu(f) - \nu(f)| \;\leq\; \inf_{(X,Y)} \; \mathop{\mathbb E}[d(X,Y)]. \ \ \ \ \ (3)

This is a deep result that on any reasonable space {(S,d)} the inequality is in fact an equality. Indeed, Kantorovich duality states that on any Radon space {(S,d)} we have

\displaystyle W(\mu,\nu) \;=\; \sup_{\text{Lip}(f) \leq 1} \; |\mu(f) - \nu(f)| \;=\; \inf_{(X,Y)} \; \mathop{\mathbb E}[d(X,Y)]. \ \ \ \ \ (4)

It is interesting to note that under mild conditions on the state space {(S,d)} one can always find a coupling that achieves the infimum of (4): this is an easy compactness argument.

2. Notion of Curvature

Denoting by {m_x = \delta_x P} the one step distribution of the Markov chain started from {x} in the sense that {m_x(A) = \mathop{\mathbb P}[X_1 \in A \;| X_0 = x ]}, we define the local (Ricci) curvature {\kappa(x,y) \in {\mathbb R}} between {x} and {y} as

\displaystyle W(m_x, m_y) = d(x,y) \cdot (1-\kappa(x,y)). \ \ \ \ \ (5)

The closer to {1} is {\kappa(x,y)}, the more the trajectories started at {x} tend to meet the trajectories started at {y}.

Trajectories tend to coalesce

The interesting case is when the infimum {\inf_{x,y} \, \kappa(x,y)} is strictly positive,

\displaystyle \inf_{x,y \in E} \kappa(x,y) \;=\; \kappa > 0. \ \ \ \ \ (6)

In this case we say that the Markov kernel {P} is positively curved on {(S,d)}. It should be noted that in many natural spaces it suffices to ensure that {\kappa(x,y) \;\geq\; \kappa} for all neighbouring states {x} and {y} to ensure that {\kappa(x,y) \;\geq\; \kappa} for any pair {x,y \in S}. This can be proved thanks to the so called Gluing Lemma. A space without curvature correspond to the case {\kappa=0}: for example, a symmetric random walk on {\mathbb{Z}^d} and a Brownian motion on {{\mathbb R}^d} have both zero curvature. The curvature {\kappa} is a property of both the metric space {(S,d)} and the Markov kernel {P}: indeed, different Markov chain on the same metric space {(S,d)} have generally different associated curvature. Given a metric space {(S,d)} carrying a probability distribution {\pi}, this is an interesting problem to construct a {\pi}-invariant Markov chain with the highest possible curvature {\kappa}.

Indeed, the notion of curvature readily generalizes to continuous time Markov processes by taking a limiting case of (5). For example, one can define the curvature of the continuous time Markov process {\{X_t\}_{t \geq 0}} as the largest real number {\kappa} such that for any {x,y \in (S,d)} and {\kappa' < \kappa} we have

\displaystyle W(m_x^{\delta}, m_y^{\delta}) \;\leq\; (1-\delta \kappa') \; d(x,y) \ \ \ \ \ (7)

for every {\delta} small enough. The quantity {m_x^{\delta}} is the distribution of {X_{\delta}} when started from {x} in the sense that {m_x^{\delta}(A) = \mathop{\mathbb P}[X_{\delta} \in A \; |X_0=x]}.

3. Contraction property

We now show that a positive curvature implies a contraction property. Equation (5) shows that {W(\delta_x P, \delta_y P) \leq W(\delta_x,\delta_y) \cdot (1-\kappa)} for any {x,y \in S}. A simple argument shows that one can indeed generalize the situation to any two distributions {\mu,\nu} in the sense that

\displaystyle W(\mu P, \nu P) \leq W(\mu,\nu) \cdot (1-\kappa). \ \ \ \ \ (8)

Proof: For any pair {x,y \in S} consider a coupling {(U_{x,y}, V_{x,y})} of {m_x} and {m_y} such that {W(m_x,m_y)=\mathop{\mathbb E}[d(U_{x,y}, V_{x,y})]}. Now, choose an optimal coupling {(X,Y)} of {\mu} and {\nu}. This is straightforward to check that {(U_{X,Y}, V_{X,Y})} is a coupling (in general not optimal) of {\mu P} and {\nu P} so that

\displaystyle \begin{array}{rcl} W(\mu P, \nu P) &\leq& \mathop{\mathbb E}[d(U_{X,Y}, V_{X,Y})] = \mathop{\mathbb E}[\; \mathop{\mathbb E}[d(U_{x,y}, V_{x,y}) \;|X=x, Y=y] ] \\ &=& \mathop{\mathbb E}[ W(m_X, m_Y) ] = \mathop{\mathbb E}[ d(X,Y) \cdot (1-\kappa(X,Y)) ]\\ &\leq& (1-\kappa) \; \mathop{\mathbb E}[ d(X,Y) ] = (1-\kappa) \; W(\mu,\nu). \end{array}

\Box

Equation (8) is extremely powerful since it immediately shows that

\displaystyle W(\mu P^t, \pi) \leq (1-\kappa)^{t} \; W(\mu,\pi). \ \ \ \ \ (9)

In other words, there is exponential convergence (in the Wasserstein metric) to the invariance distribution {\pi} at rate {(1-\kappa)^t}. In continuous time, this reads

\displaystyle W(\mu P^t, \pi) \;\leq\; e^{-\kappa t} \; W(\mu,\pi). \ \ \ \ \ (10)

In other words, the higher the curvature, the faster the convergence to equilibrium.

4. Examples

Let us give examples of positively curved Markov chains.

  1. Langevin diffusion with convex potential: consider a convex potential {\Psi:{\mathbb R} \rightarrow {\mathbb R}} that is uniformly elliptic in the sense {\Psi^{''}(x) \geq \lambda > 0}. The Langevin diffusion {dz = -\frac{1}{2} \Psi'(z) \, dt + dW} has invariant distribution {\pi} with density proportional to {e^{-\Psi(x)}}. Given a time step {\delta}, the Euler discretization of this diffusion reads
    \displaystyle x^{k+1} = x^k - \frac{1}{2} \Psi'(x^k) \, \delta + \sqrt{\delta} \; \xi \ \ \ \ \ (11) 

    where {\xi \sim {\mathcal N}(0,1)}. Given two starting points {x^0=x} and {y^0=y}, using the same noise {\xi} to define {x^1} and {y^1} it immediately follows that

    \displaystyle \begin{array}{rcl} W(x^1, y^1) &\leq& (x-y) \; \Big(1 - \frac{\delta}{2} \frac{\Psi'(x)-\Psi'(y)}{x-y} \Big)\\ &\leq& (x-y) \; (1-\frac{\lambda}{2} \delta). \end{array}

    In other words, the Langevin diffusion {\{z_t\}_{t \geq 0}} is positively curved with curvature (at least) equal to {\kappa = \frac{\lambda}{2}}.

     

  2. Brownian motion on a sphere: consider a Brownian motion on the unit sphere of {{\mathbb R}^n}. Consider two points {X,Y} on this unit sphere: by symmetry, one can always rotate the coordinates so that that {X=(\sqrt{1-h^2},0,h)} and {X=(\sqrt{1-h^2},0,-h)} for some {h \in [0,1]}. For {h \ll 1} the (geodesic) distance {d(X,Y)} is approximated by {d(X,Y) \approx 2h}. One can couple two Brownian motions {W^X} and {W^Y}, one started at {X} and the other one started at {Y}, by the usual symmetry with respect to the plane {\mathcal{P} = \{(x,y,z): z=0\}}: in other words, {W^Y} is the reflexion of {W^X} with respect to {\mathcal{P}}. One can check (good exercise!) that the diffusion followed by the {z}-coordinate of a Brownian motion on the unit sphere of {{\mathbb R}^n} is simply given by
    \displaystyle dz = -\frac{1}{2}(n-1)z \, dt + \sqrt{1-z^2} \, dW. \ \ \ \ \ (12) 

    With this coupling, for small time {\delta \ll 1}, it follows that

    \displaystyle \begin{array}{rcl} z^X_{\delta} &\approx& h - \frac{1}{2} (n-1) h \, \delta + \sqrt{1-h^2} \sqrt{\delta} \; \xi\\ z^Y_{\delta} &\approx& -h + \frac{1}{2} (n-1) h \, \delta - \sqrt{1-h^2} \sqrt{\delta} \; \xi \end{array}

    where {\xi \sim {\mathcal N}(0,1)} is used as the same source of randomness for {z^X_{\delta}} and {z^Y_{\delta}} since {W^Y} is the reflexion of {W^X}. Since {d(W^X_{\delta}, W^X_{\delta}) \approx |z^X_{\delta} - z^Y_{\delta}|} it readily follows that

    \displaystyle \begin{array}{rcl} d(W^X_{\delta}, W^X_{\delta}) \; \leq \; \big(1- \frac{1}{2}(n-1)\delta \big)\; d(x,y). \end{array}

    In other words, the curvature of a Brownian motion on the unit sphere of {{\mathbb R}^n} is equal to {\frac{1}{2}(n-1)}. Maybe surprisingly, the higher the dimension, the faster the convergence to equilibrium. This is not so unreal if one notices that the Brownian increment satisfies {\mathop{\mathbb E} \|W_{t+\delta}-W_t\|^2 \approx n \delta}.

  3. Other examples: see the original text for many other examples.

6 Comments

Random permutations and giant cycles

June 3, 2010 at 11:07 pm (coagulation, fluid limit, fragmentation, markov chain, probability, random permutation)
Tags: , , , , ,

The other day, Nathanael Berestycki presented some very nice results on random permutations. Start with the identity permutation of {\mathfrak{S}_N} and compose with random transpositions: in short, at time {k} we consider the random permutation {\sigma_k = \tau_k \circ \ldots \tau_{2} \circ \tau_1} where {\tau_i} is a transposition chosen uniformly at random among the {\frac{N(N-1)}{2}} transpositions of {\mathfrak{S}_N}. How long do we have to wait before seeing a permutation that has a cycle of length greater than {\epsilon N}, where {\epsilon>0} is a fixed constant ?

The answer has been known for quite a long time (O. Schramm,2005), but no simple proof was available: the highlight of Nathanael’s talk was a short and elegant proof of the fact that we only have to wait a little bit more than {N/2} steps to see this giant cycle! The first half of the proof is such a beauty that I cannot resist in sharing it here!

1. Visual representation

First, this is more visual to represent a permutation by its cycle decomposition. Consider for example the permutation {\sigma = (1,3,4)(5,6,8,9,10,11)(2)(7) \in \mathfrak{S}_{10}} that sends {1 \rightarrow 3 \rightarrow 4 \rightarrow 1} etc… It can be graphically represented by the following pictures:

cycle structure - visual representation

cycle structure - visual representation

If this permutation is composed with the transposition {(4,6)} , this gives the following cycle structure:

two cycles merge

two cycles merge

If  it is composed with {(8,11)} this gives,

a cycles breaks down into two

a cycles breaks down into two

It is thus pretty clear that the cycle structure of {\sigma_{k+1}} can be obtained from the cycle structure of {\sigma_k} in only 2 ways:

  • or two cycles of {\sigma_k} merge into one,
  • or one cycle of {\sigma_k} breaks into two cycles.

In short, the process {\{\sigma_k\}_k} behaves like a fragmentation-coalescence processes. At the beginning, the cycle structure of {\sigma_0=\text{Id}} is trivial: there are {N} trivial cycles of length one! Then, as times goes by, they begin to merge, and sometimes they also break down. At each step two integers {i} and {j} are chosen uniformly at random (with {i \neq j}): if {i} and {j} belong to the same cycle, this cycle breaks into two parts. Otherwise the cycle that contains {i} merges with the cycle that contains {j}. Of course, since at the beginning all the cycles are extremely small, the probability that a cycles breaks into two part is extremely small: a cycle of size {k} breaks into two part with probability roughly equal to {\Big(\frac{k}{N}\Big)^2}.

2. Comparison with the Erdos-Renyi random Graph

Since the fragmentation part of the process can be neglected at the beginning, this is natural to compare the cycle structure at time {k} with the rangom graph {G(N,p_k)} where {\frac{N(N-1)}{2}p_k = k}: this graph has {N} vertices and roughly {k} edges since each vertex is open with probability {p_k}. A coupling argument makes this idea more precise:

  1. start with {\sigma_0=\textrm{Id}} and the graph {G_0} that has {N} disconnected vertices {\{1,2, \ldots, N\}}
  2. choose two different integers {i \neq j}
  3. define {\sigma_{k+1}=(i,j) \circ \sigma_k}
  4. to define {G_{k+1}}, take {G_k} and join the vertices {i} and {j} (never mind if they were already joined)
  5. go to step {2}.

The fundamental remark is that each cycle of {\sigma_k} is included in a connected component of {G_k}: this is true at the beginning, and this property obviously remains true at each step. The Erdos-Renyi random graph {G(n,p)} is one of the most studied object: it is well-known that for {c<1}, with probability tending to {1}, the size of the largest connected component of {G(N,\frac{c}{N})} is of order {\ln(N)}. Since {p_k \sim \frac{2k}{N^2}}, this immediately shows that for {k \approx \alpha N}, with {\alpha < \frac{1}{2}} the length of the longuest cycle in {\sigma_k} is of order {\ln(N)} or less. This is one half of the result. It remains to work a little bit to show that if we wait a little bit more than {\frac{N}{2}}, the first cycle of order {N} appears.

For a permutation {\sigma \in \mathfrak{S}_N} with cycle decomposition {\sigma = \prod_{j=1}^r c_i} (cycles of length {1} included), one can consider the quantity

\displaystyle T(\sigma) = \sum_{j=1}^R |c_j|^2.

This is a quantity between {N} (for the identity) and {N^2} that measures in some extends the sizes of the cycles. In order to normalize everything and to take into account that the cycle structure abruptly changes near the critical value {\frac{N}{2}}, one can also observe this quantity on a logarithmic scale:

\displaystyle s(\sigma) = \frac{ \ln\Big( T(\sigma)/N^2 \Big) }{\ln(N)}.

This quantity {s(\sigma)} lies between {0} and {1}, and evolves quite smoothly with time: look at what it looks like, once the time has been rescaled by a factor {N}:

fluid limit ?

fluid limit ?

The plot represented the evolution of the quantity {s\Big(\sigma(\alpha N)\Big)} between time k=0 and k=\frac{N}{2} for dimensions N=10000,20000,30000.

Question: does the random quantity s(\alpha,N)={s\Big(\sigma(\alpha N)\Big)} converge (in probability) towards a non trivial constant {S(\alpha) \in (0,1)} ? It must be the analogue quantity for the random graph {G(N,\frac{2\alpha}{N})}, so I bet it is a known result …

1 Comment